Okab, Zeta Aquilae A (ζ Aql A), is the primary component in a binary star system located approximately 83 light years away in the constellation Aquila. With an apparent magnitude of 2.983, it is the third brightest star in Aquila, after Altair and Tarazed. In traditional depictions of the constellation, Okab marks the tail of the celestial Eagle.
Star system
Zeta Aquilae is a binary star consisting of Zeta Aquilae A (formally named Okab), a white star of the spectral type A0IV-Vnn, and Zeta Aquilae B, a magnitude 12.0 star separated by 7.20 arcseconds from the primary. The physical separation between the two components is 185.1 astronomical units (Earth-Sun distances).
Classified as either a main sequence star or a subgiant, Zeta Aquilae A is coming to the end of its main sequence lifetime and if it has not already run out of hydrogen to fuse in its core, it will soon do so. It has a mass 2.37 times that of the Sun and a radius 2.27 times solar. With an effective temperature of 9,620 K, it is 39.4 times more luminous than the Sun. Its estimated age is about 100 million years (with a margin of error of 50 million years).

Okab (Zeta Aquilae), image: Wikisky
Okab is an exceptionally fast spinner, with a projected rotational velocity of 317 km/s. The star’s fast spin rate has distorted its shape into an oblate spheroid. As a result, Okab’s radius at the equator is about 30.7% greater than its radius at the poles.
The companion, Zeta Aquilae B, is considerably less massive, with only 50% of the Sun’s mass.
The Washington Double Star Catalog lists five components in the Zeta Aquilae system, which has the designation WDS J19054+1352. As the primary star, Okab is designated as WDS J19054+1352A and the four companions as components B, C, D, and E. The visual magnitudes of the companions, as given, are 12.00 (WDS J19054+1352B), 12.20 (C), 10.65 (D), and 16.20 (E). The faintest of these stars, WDS J19054+1352E, is believed to be moving through space with Zeta Aquilae A and B. The star has a mass only 14% that of the Sun and is separated by 38,000 astronomical units from Zeta Aquilae A.
The Catalog of Components of Double & Multiple Stars (CCDM) lists only two companions, CCDM 19055+1352B with an apparent magnitude of 12.0, separated by 6.5 arcseconds from the primary, and CCDM 19055+1352C with a visual magnitude of 11.8, at a separation of 158.6 arcseconds.
Facts
Okab is a candidate member of the TW Hydrae association, the youngest such association within 100 parsecs of the Sun. The members of the group are young, low-mass stars that lie at distances from 80 to 240 light years from Earth. They were formed in the same molecular cloud and are about 10 million years old. They share a common motion through space. The confirmed members have masses in the range from 5 Jupiter masses to 2 solar masses, and their spectral types range from A0 to L7. The group was named after TW Hydrae in the constellation Hydra, the nearest T Tauri star (variable pre-main-sequence star) to Earth, located 196 light years away.
Name
The name Okab (pronunciation: /ˈoʊkæb/) comes from the star’s traditional name, Deneb el Okab, meaning “the tail of the eagle.” While observers may assume that Zeta Aquilae marks the Eagle’s wing and Lambda Aquilae the tail, in traditional depictions of the constellation, Zeta and the orange giant Epsilon Aquilae mark the bird’s tail. The two stars were traditionally known as Deneb el Okab Australis (Zeta) and Deneb el Okab Borealis (Epsilon).
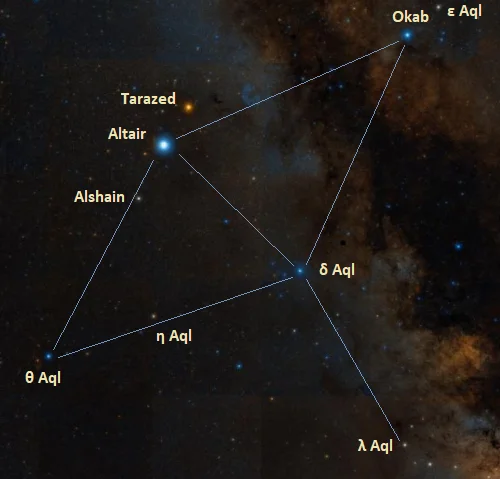
Aquila stars, image: Wikisky
The name Okab was approved by the International Astronomical Union’s (IAU) Working Group on Star Names (WGSN) on June 1, 2018. It formally applies only to the component Zeta Aquilae A.
Okab was also traditionally known as Dzeneb al Tair, “the eagle’s tail.” The name appeared in the 17th century Egyptian astronomer Al Achsasi Al Mouakket’s Calendarium. It was later translated into Latin as Cauda (Vulturis) Volantis. (In Roman times, the constellation Aquila was also known as Vultur volans, meaning “the flying vulture.”)
The Chinese know Okab as 天市左垣六 (Tiān Shì Zuǒ Yuán liù), the Sixth Star of Left Wall of Heavenly Market Enclosure. The Chinese asterism called Left Wall of Heavenly Market Enclosure is formed by Okab with Sarin (Delta Herculis), Maasym (Lambda Herculis), Mu Herculis, Omicron Herculis, 112 Herculis, Alya (Theta Serpentis), Eta Serpentis, Mu Ophiuchi, Xi Serpentis, and Sabik (Eta Ophiuchi). The asterism is part of the Heavenly Market Enclosure, one of the three enclosures in Chinese astronomy, which represents the emperor’s realm. The stars of the Left Wall represent 11 cities in the left.
Epsilon and Zeta Aquilae were known by the Mandarin names Wu and Yue, as they represented the two old states, Wu (located at the mouth of the Yangtze River) and Yue (located in the modern provinces of Zhejiang, Shanghai and Jiangsu).
Location
Okab is easy to find because it is part of Aquila’s distinctive bird-like pattern. It can be found using two bright summer asterisms: the Northern Cross and the Summer Triangle. The Summer Triangle is formed by Altair with Vega and Deneb, the brightest stars in the constellations Lyra and Cygnus. The asterism dominates the evening sky, appearing high overhead during the northern hemisphere summer. Deneb sits at the top of the Northern Cross and marks the tail of the celestial Swan (Cygnus), while the fainter Albireo, the star at the base of the Cross, marks the Swan’s beak. A line extended from Deneb through Albireo points roughly in the direction of Okab.
Okab can also be identified by simply finding the pattern of Aquila. The Eagle appears just opposite the more conspicuous Swan in the sky, with the birds’ heads facing each other. Okab appears at the Eagle’s right wing.
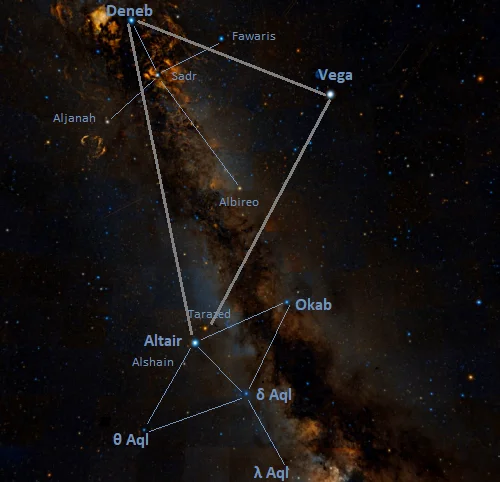
The location of Okab, image: Wikisky
Constellation
Okab is located in the northern constellation Aquila. Aquila occupies 652 square degrees and is the 22nd constellation in size. It is easy to identify because its brightest stars form the shape of a bird with outstretched wings, flying opposite the celestial Swan (Cygnus). The Eagle’s head (or neck) is marked by Altair, the 12th brightest star in sky and one of our nearest neighbours.
Aquila was first catalogued by the Greek astronomer Ptolemy in his Almagest in the 2nd century BC and is considered to be one of the 48 Greek constellations. In mythology, it is associated with two eagles: the eagle that carried Zeus’ thunderbolts and the one that carried the young Ganymede (represented by Aquarius) to Mount Olympus to serve as cupbearer to Zeus and other Olympian gods.

Aquila constellation map by IAU and Sky&Telescope magazine
Aquila is best-known for being home to the bright Altair, a white Delta Scuti variable only 16.73 light years from the Sun. The constellation contains many other notable stars, among them the orange bright giant Tarazed (Gamma Aquilae), the triple star system Beta Aquilae (Alshain), the semiregular variable carbon star V Aquilae, the orange giant Epsilon Aquilae, and the Cepheid variable Eta Aquilae.
Relatively bright deep sky objects in the constellation include the open clusters NGC 6709, NGC 6755 and NGC 6749, the globular cluster NGC 6760, and the planetary nebulae NGC 6751 (the Glowing Eye Nebula), NGC 6741 (the Phantom Streak Nebula), NGC 6781 (the Snowglobe Nebula), NGC 6778, and NGC 6804. The constellation also hosts the protoplanetary Starfish Nebula, the supernova remnant Westerhout 50 (the Manatee Nebula), and the dark E Nebula (Barnard 142 and 143).
The best time of year to observe the stars and deep sky objects of Aquila is during the month of August, when the constellation is high overhead in the evening sky for northern observers. The entire constellation is visible from locations between the latitudes 90° N and 75° S.
The 10 brightest stars in Aquila are Altair (Alpha Aql, mag. 0.76), Tarazed (Gamma Aql, mag. 2.712), Okab (Zeta Aql, mag. 2.983), Theta Aquilae (mag. 3.26), Delta Aquilae (mag. 3.365), Lambda Aquilae (mag. 3.43), Alshain (Beta Aql, mag. 3.87), Eta Aquilae (mag. 3.87), Epsilon Aquilae (mag. 4.02), and 12 Aquilae (mag. 4.02).
Okab – Zeta Aquilae
| Spectral class | A0IV-Vnn |
| U-B colour index | +0.080 |
| B-V colour index | +0.009 |
| Apparent magnitude | 2.983 |
| Absolute magnitude | +0.96 |
| Distance | 83.0 ± 0.3 light years (25.5 ± 0.1 parsecs) |
| Parallax | 39.28 ± 0.16 mas |
| Radial velocity | -25 ± 4 km/s |
| Proper motion | RA: -7.25 ± 0.15 mas/yr |
| Dec.: -95.56 ± 0.12 mas/yr | |
| Mass (ζ Aql A, ζ Aql B) | 2.37 M☉, 0.50 M☉ |
| Luminosity (ζ Aql A) | 39.4 L☉ |
| Radius (ζ Aql A) | 2.27 R☉ |
| Temperature (ζ Aql A) | 9,620 ± 20 K |
| Metallicity (ζ Aql A) | −0.52 ± 0.04 dex |
| Age (ζ Aql A) | 100 ± 50 million years |
| Rotational velocity (ζ Aql A) | 317 km/s |
| Surface gravity (ζ Aql A) | 4.17 cgs |
| Constellation | Aquila |
| Right ascension | 19h 05m 24.6080155s |
| Declination | +13° 51′ 48.518212″ |
| Names and designations | Okab, Zeta Aquilae, ζ Aql, 17 Aquilae, HD 177724, HR 7235, HIP 93747, SAO 104461, FK5 716, GC 26270, GCRV 11547, BD+13 3899, AG+13 1887, GJ 4095, PPM 135773, GSC 01052-03027, PLX 4436.00, EUVE J1905+13.8, IRAS 19031+1347, 2MASS J19052461+1351486, JP11 3072, UBV 16191, TYC 1052-3027-1, Gaia DR2 4314399312929014656WDS J19054+1352A, ADS 12026 A, CCDM J19055+1352A, IDS 19008+1343 A, WDS J19054+1352A |